Úvod
Pýtate sa, čo tieto obrázky majú s témou spoločné? Nuž na prvý pohľad málo, no aj pri prvočíslach ide o kľúčovú otázku. Je za tým God of chaos or God of structure? Môžeme ich aj premenovať na Boha entropie a Boha fraktálov.
V minulých dieloch Prvočísla diel 1, Prvočísla diel 2, Prvočísla diel 3 sme stručne prebrali dôležité súvislosti s prvočíslami a Riemanovou hypotézou. Z týchto informácii, aj keď nie su rozobrané do najmenších podrobnosti sa dá usúdiť, že Riemannova hypotéza je prakticky dokázaná. Pre naozaj veľké čísla sú stále korene na kritickej priamke.
V podstate skutočný dôkaz pre celú číselnú os nám nemusí priniesť nejaké ďalšie nepoznané súvislosti pre prvočísla. Myslím si, že nám môže priniesť iba to, že naozaj to pokračuje na tej kritickej priamke ľubovoľne ďaleko.
Tak som sa rozhodol, keď už som tomu venoval nejaký ten čas na preštudovanie tejto hypotézy, že budem v rámci možnosti času a chuti pokračovať v hľadaní nie dôkazu Riemannovej hypotézy, ale toho, či prvočísla vykazujú fraktálnu štruktúru, pattern, vzorec, nech už si to nazveme akokoľvek...
Prvý odhad
Zdá sa, že tam nejaká schéma funguje, no obávam sa, že pri jemnom delení (teda, či práve toto číslo je prvočíslo) narazíme na problém chaosu.
O tom čo je to vlastne chaos a čo poriadok som sa venoval v článkoch v minulosti a hlavne v Knihe EDQ teórie o priestore a čase (nájdete v eshope).
Odhad človeka je výsledkom jeho neurónovej siete, skúsenosti, vedomosti. Prvočísla sú naozaj ťažký problém, ktorý odoláva času. Teda dobré vysvetlenie (odhad) je to, že za tým je schovaný aj chaos. Myslené je to tak, že predvídanie prvočísiel nevykazuje žiaden jednoznačný opakujúci sa vzor (jednoducho spočitatelný). Čo to vlastne je chaos? Pod chaosom si predstavujú ľudia rôzne veci..
Tento článok je vlastne takým úvodom do vlastného, súkromného bádania po fraktáloch prvočísiel. No samozrejme je celkom možné, že to vzdám, resp. ma zaujme niečo iné a nebudem sa tomu venovať ďalej.
Viem si celkom dobre predstaviť použitie zbrane hromadného ničenia - teda umelej neuronóvej siete, ktorá bude prehľadávať stavový priestor, kým nenájde fraktály. Nechajme ju predvídať, ktoré číslo bude prvočíslo a ona sa to v budúcnosti možno naučí. Bohužial ten "pattern", ktorý nájde bude v inej forme jej schémy zakódovaný (pojde to, ale rozkódovať do matematických vzťahov), no bude to aspoň niečo...
Takéhoto pomocníka nemám, problém je naozaj veľmi obťiažny, takže uvidíme..
Mersennovo prvočíslo
Zastavme sa ešte na chvíľu pri tzv. Mersennovom prvočísle, ktoré je definované predpisom:Zoznam Mersennových prvočísiel nájdete na wikipédii (vrátane najväčšieho známeho prvočísla). Táto formula však negeneruje len prvočísla, príkladom je:
Teda to nie je jednoznačný pattern.
Godlbachova domnienka
O niečo jednoduchší problém je tzv. Goldbachová domnienka, ktorá sa formuluje:
- Každé párne celé číslo väčšie ako 2 sa dá vyjadriť ako súčet dvoch prvočísel. Táto domnienka sa dá pekne geometricky interpretovať, znázorniť.
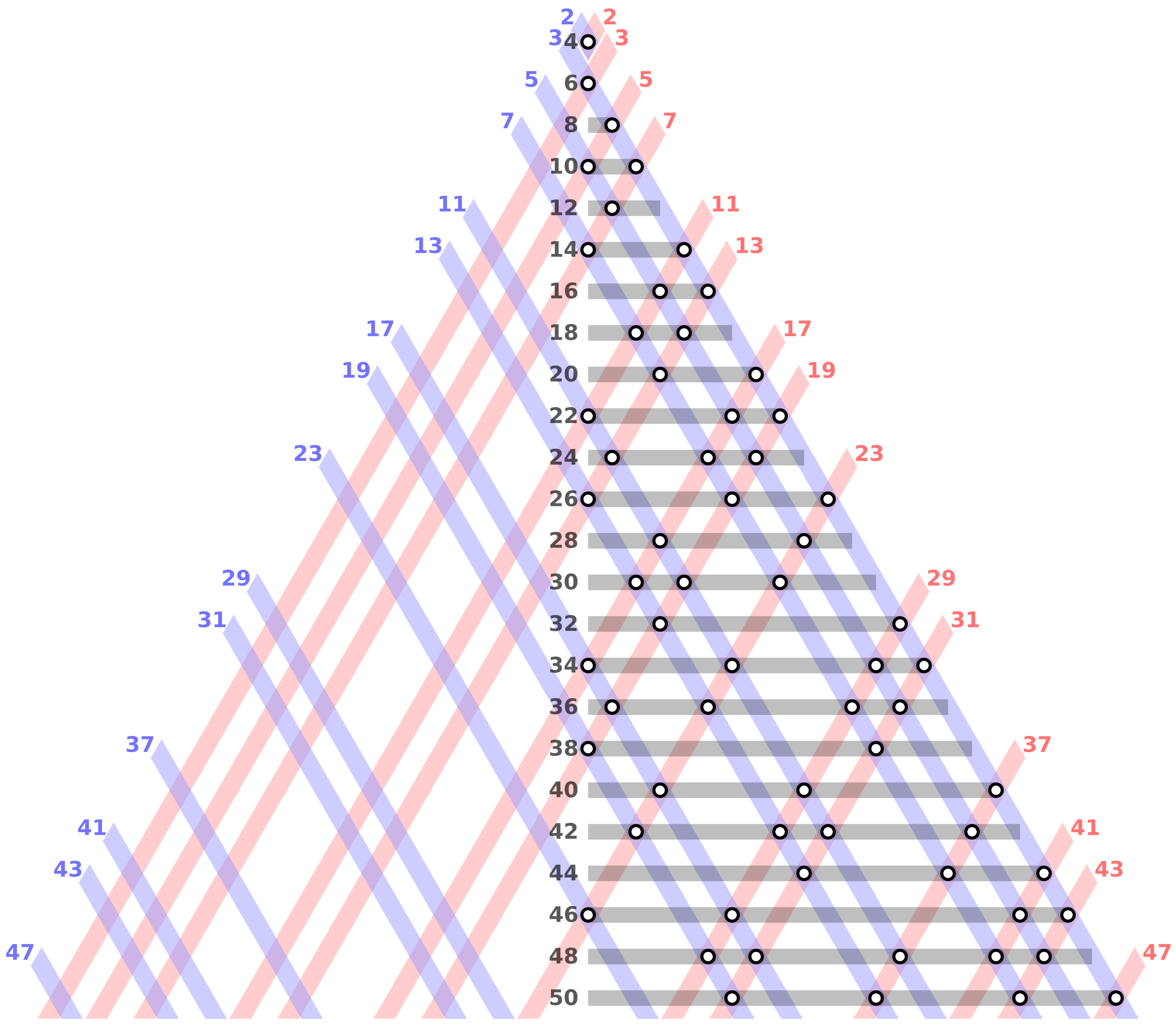
Obr.2 Goldbachová domnienka, zdroj: wikipédia.
Ku Goldbachovej hypotéze sa vrátim neskôr.
Základné vlastnosti prvočísiel
Vráťme sa znova k základným vlastnostiam prvočísiel a k tvrdeniam: z článku Prvočísla – Riemannova hypotéza – 2. diel.
Vlastnosť:
- Každé zložené číslo sa dá rozložiť na súčin prvočísiel.
- Tvrdenie B.
Toto tvrdenie vlastne hovorí, že na to, aby sme vedeli rozhodnúť, či je práve toto číslo prvočíslo musíme poznať predchádzajúce prvočísla.
Z toho sa dá usúdiť, že nejaký jednoduchý vzťah pre hľadanie prvočísiel je nepravdepodobný. Ilustrujeme si toto tvrdenie na geometrickom obrázku plochy o veľkosti – S, ktorá ma vždy celočíselný obsah.
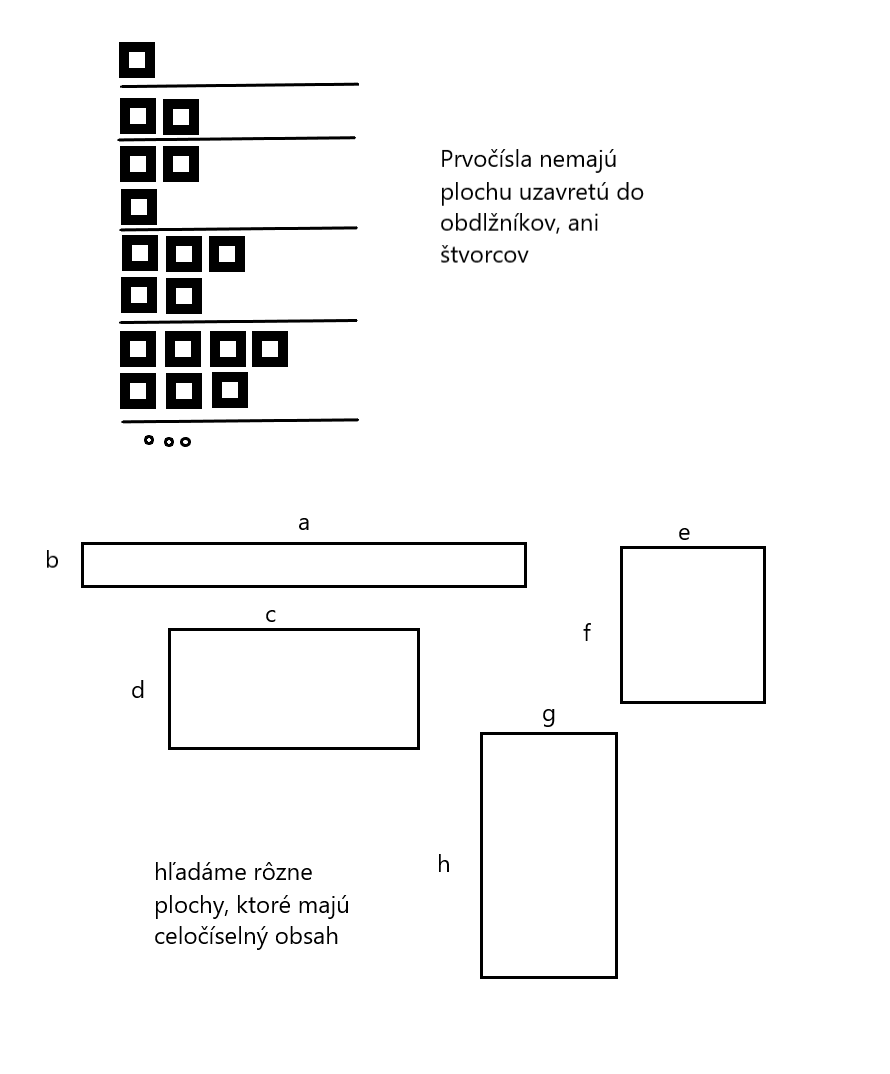
Obr.3 Plocha prvočísiel, zdroj: vlastný obrázok.
Teda hľadáme plochu obdĺžnika (platí pre zložené číslo)
- S(x,y)=x*y, pričom x,y sú celočíselné premenné. Takýmto spôsobom pre veľké číslo dostaneme rôzne obdĺžniky o rôznych stranách. U zložených čísiel teda vždy existuje aspoň jeden obdĺžnik o hrane x, y.
- Pre prvočísla však neexistuje ani jeden obdĺžnik x, y, okrem obdĺžnika, ktorý ma jednu hranu „1“.
- Každý obdĺžnik (teda zložené číslo) nakoniec rozbijeme na menšie obdĺžniky, kde hrany obdĺžnikov budú práve prvočísla:
Príklad:
S(99)=33*3
S(33) rozbijeme na S(33)=3*11
Teda celú plochu S(99) rozbijeme na 3 obdĺžniky o hrane (3,11).
Z toho teda plynie toto:
Ak chceme prehlásiť, či je niektoré, skúmané číslo prvočíslo - n, musíme toto číslo podeliť všetkými, predchádzajúcimi prvočíslami (min do 1/3n, dá sa to zistiť presne). Ak výsledok podielu nie je ani raz celé číslo, potom skúmané číslo je prvočíslo.
Ani R(x): Riemannova funkcia (viď. diel 2) nie je jednoduchá čarovná formula, ale je definovaná ako nekonečný rad funkcie Li(x). Zatiaľ nemám znalosti ako rýchlo konverguje funkcia R(x). Z toho, čo som sa dočítal konverguje celkom rýchlo. V tom prípade by Riemanová funkcia R(x) aproximala prvočísla rýchlejšie ako Eratostenovo sito, skúsim to v budúcnosti preskúmať detailnejšie.
Energetické hladiny elektrónov súvisia s prvočíslami, pretože Kvantový svet je diskrétny, teda ako keby celočíselný, čo úzko súvisí s prvočíslami.
Pri takomto algoritme potrebujeme zoznam prvočísiel, pričom nemusíme deliť dvojkou, ani päťkou. Dvojkou netreba, lebo nepárne číslo sa nedá rozdeliť dvojkou na celočíselný násobok, päťkou netreba, pretože čísla končiace päťkou nemôžu byť prvočísla.
Pozrime sa na to ako to vyzerá v nejakej malej škále čísiel s rozmiestnením:
http://hradec.org/idnes/primes.html
Na väčšej škále:
napr. obrázok Ulamovej špirály : Prvočísla, diel 3.
Na prvý pohľad sa tam neopakuje žiaden vzor, no toto by bolo najlepšie preskúmať cez počítač, ktorý by prešiel rôzne dlhé reťazce. Predpokladám, že niekto toto už skúšal a nič také nenašiel, nejaký vzor s nejakou periódou opakujúci sa neustále ďalej. Pre náročnosť takéhoto hľadania, to skúmať osobne nebudem. Navyše by vzor riedol s funkciou x/lnx (Gauss).
Malá Fermatova veta
Ide o túto formulu: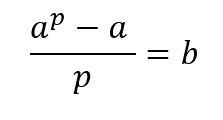
Pričom :
a - je celé číslo, p - je prvočíslo, b - je celé číslo.
Príklad:
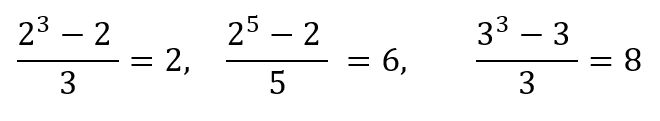
Wolfram príklad (môžete meniť premenné):
https://www.wolframalpha.com/input/?i=%285%CB%8617-5%29%2F17Zovšeobecnením malej Fermatovej vety bol vytvorený účinný algoritmus AKS - algoritmus, pre hľadanie prvočísiel. Pričom AKS má polynomionálnu zložitosť pre ľubovolný vstup.
Prehľad algoritmov
- Lucas -Lehmerov test.
- Rabin - Millerov test.
- ECPP.
- iné.
http://thales.doa.fmph.uniba.sk/sleziak/papers/aks.pdf

Obr.4 AKS - algoritmus, zdroj: fmph.uniba.sk
Dôkazy malej Fermatovej vety
Ešte predtým, ako napíšem nejaké dôkazy k malej Fermatovej vete musím konštatovať, že táto veta je naozaj veľmi nápomocná pri hľadaní prvočísiel. Táto vlastnosť poskytuje výhodu pri určovaní prvočísiel. Neskôr doplním vlastne úvahy s malou Fermatovou vetou (diel 5).Dôkaz malej Fermatovej vety urobil napr. Euler, dôkazy nájdete na internete, napr. aj v poslednom linku (prehľad algoritmov).
Malú Fermatovú vetu spĺňajú aj niektoré, zložené čísla, preto je potrebné nájsť optimálny algoritmus. V podstate tu, ale platí, že zložené číslo sa odhalí pre rôzne "a" , pretože podmienku spĺňa, iba pre niektoré a=2,3....n.
Pár zaujímavosti:
- Výsledkom vzťahu, pokiaľ je splnená podmienka p= prvočíslo, no platí to aj pre zložené čísla, potom výsledok vzťahu je vždy párne číslo. Nutná a postačujúca podmienka je, aby výsledkom vzťahu bolo celé číslo.
Dôkaz:

-- pokračovanie v ďalšom diely o prvočíslach ---
